원광성
탄도방정식과 이차함수, 학교폭파에 관하여 본문
0. 서론
동래역 4번 출구에 살던 김모씨(16세, 미필)은 매일 등교하던 어느 날 학교에 가기 싫어 졌다.
따라서 게임 속 군대에 있을 때 사용하던 81mm 박격포를 이용하여 자신이 다니는 학교인 부산대학교를 날려버리는 계획을 세우게 되는데...


※ 주의 ※
이 글에 등장하는 모든 인물, 이름, 집단, 사건은 허구이며 실존하는 인물, 장소, 건물과는 일절 관련이 없습니다.
주인장은 부산대를 다니지도 동래역 4번 출구에 살지도, 성이 김씨도 17세도 아닙니다.
또한 부산대를 폄하할 의도가 없음을 알립니다.
1. 이론
우리는 발사 지점과 표적 간의 상대적 거리와 고도차, 포탄의 포구속도를 알고 있습니다.
여기에서 박격포의 고도각을 몇 도로 조준하여야 동래역 4번 출구에서 부산대학교를 날려버릴 수 있는지 구하는 것이 목표입니다.

위 그림과 같이 포구속도가 $v_0$인 포탄이 좌표 $(0,0)$에서 $\theta$의 각도로 날라가면 x방향으로는 $v_0\cos\theta$의 속도로 y방향으로는 $v_0\sin\theta$의 속도로 날라갑니다.
이때 시간 $t$에 따라 포탄의 위치를 $x, y$라 하면 $$x = v_0t\cos\theta\tag{1}$$ $$y = v_0t\sin\theta - \frac{g}{2}t^2\tag{2}$$라는 공식이 나오게 됩니다. ($g$는 중력가속도 이다.)
그 이유는 고등학교 '물리Ⅰ' 에 나오는 등속도 운동/등가속도 운동을 참조하자
식 1을 $t$에 대하여 정리하여 식 2에 넣으면 다음과 같은 식이 됩니다.
$$y=x\tan\theta-\frac{g}{2}\cdot\frac{x^2}{v_0^2}\cdot\sec^2x$$
$$y=x\tan\theta-\frac{g}{2}\cdot\frac{x^2}{v_0^2}-\frac{g}{2}\cdot\frac{x^2}{v_0^2}\cdot\tan^2\theta \tag{3} $$
위의 식에 따르면 포탄은 이차함수의 모양으로 날아간다는 것을 알 수 있습니다.
또한 $(0,0)$에서 발사하였기 때문에 원점을 지난다는 것도 알 수 있습니다.
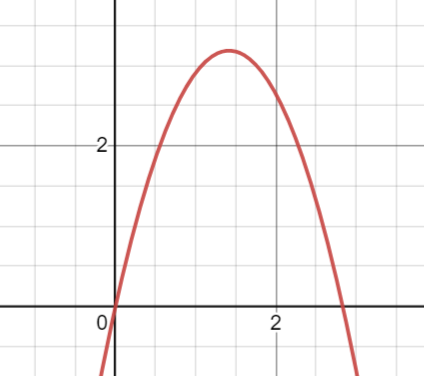
식3에서 3개의 변수$x,\:y,\:\theta$가 존재하는데 $x$와 $y$에는 표적의 상대 거리와 고도차인 $ x_0,\:y_0$를 넣어서 $\tan\theta$에 관한 이차식으로 만들 수 있습니다.
$$\frac{gx_0^2}{2v_0^2}\tan^2\theta - x_0\tan\theta+\frac{gx_0^2}{2v_0^2} + y_0 = 0 \tag{4} $$
위의 식을 근의 공식을 이용하여 $\tan\theta$를 구하면
$$\tan\theta = \frac{x_0\pm\sqrt{x_0^2 - 2g\cdot\frac{x_0^2}{v_0^2}\cdot(\frac{gx_0^2}{2v_0^2}+y_0)}}{g\cdot\frac{x_0^2}{v_0}}$$
위와 같이 $\tan\theta$에 관한 식 2개가 나오게 됩니다.
우리가 구한 $\tan\theta$에다 아크 탄젠트를 씌우면 우리가 필요한 세타값을 얻을 수 있습니다.
2개의 각은 각각 고각과 저각으로 발사한 것입니다.
우리는 박격포를 이용할 것인데 박격포는 보통 고각으로 발사하니 두 개의 세타값중 큰 것만 취하면 됩니다.
2. 적용
이제 우리는 학교를 날리기 위한 준비가 되었습니다.
위 식에 필요한 변수는 발사 지점과 표적 간의 상대적 거리와 고도차, 포탄의 포구속도입니다.
위키백과에서 얻은 M1 박격포 포구속도는 210m/s.
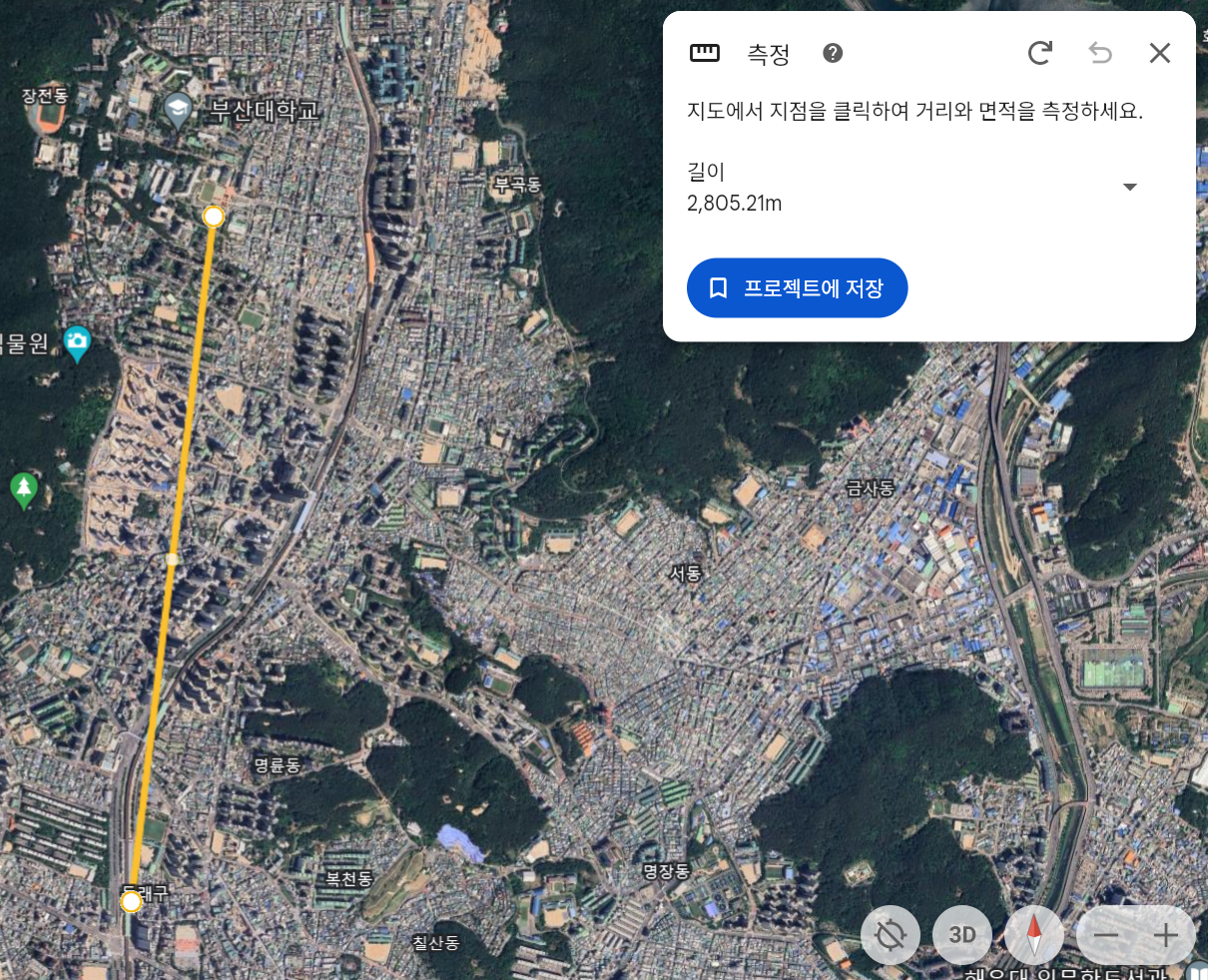
구글 어스에서 자대고 측정한 상대 x거리는 2,805m, 상대 y거리(고도차)는 30m입니다.
고도차 = (부산대학교 해발고도 = 43m) - (동래역 해발고도 = 13m) = 30m
$$\tan\theta = \frac{x_0\pm\sqrt{x_0^2 - 2g\cdot\frac{x_0^2}{v_0^2}\cdot(\frac{gx_0^2}{2v_0^2}+y_0)}}{g\cdot\frac{x_0^2}{v_0}}$$
이제 위의 식을 풀어야 하지만 너무 귀찮은 관계로 c언어를 이용하여 코드를 짜서 구해봅시다.
#include <stdio.h>
#include <math.h>
int main(void) {
double g, h2, h1, v, a1, a2, n1, n2, pi ;
pi = 3.1415926535;
g = 9.80665;
printf("표적과의 수평거리를 입력하세요. (h1)(단위 = m)");
scanf("%lf", &h1);
printf("표적과의 수직거리를 입력하세요. (h2)(단위 = m)");
scanf("%lf", &h2);
printf("포탄의 포구속도를 입력하세요. (단위 = m/s)");
scanf("%lf", &v);
a1 = ((h1*pow(v,2))+sqrt(-pow(h1,2)*((pow(g,2)*pow(h1,2))+(2*g*h2*pow(v,2))-pow(v,4))))/(g*pow(h1,2));
a2 = ((h1*pow(v,2))-sqrt(-pow(h1,2)*((pow(g,2)*pow(h1,2))+(2*g*h2*pow(v,2))-pow(v,4))))/(g*pow(h1,2));
printf("tan(a) = %lf or %lf\n", a1, a2);
n1 = atan(a1);
n2 = atan(a2);
printf("a = %lf or %lf", n1*180/pi, n2*180/pi);
getch();
return 0;
}
위의 코드를 이용하여 적절한 세타값을 구해보면...
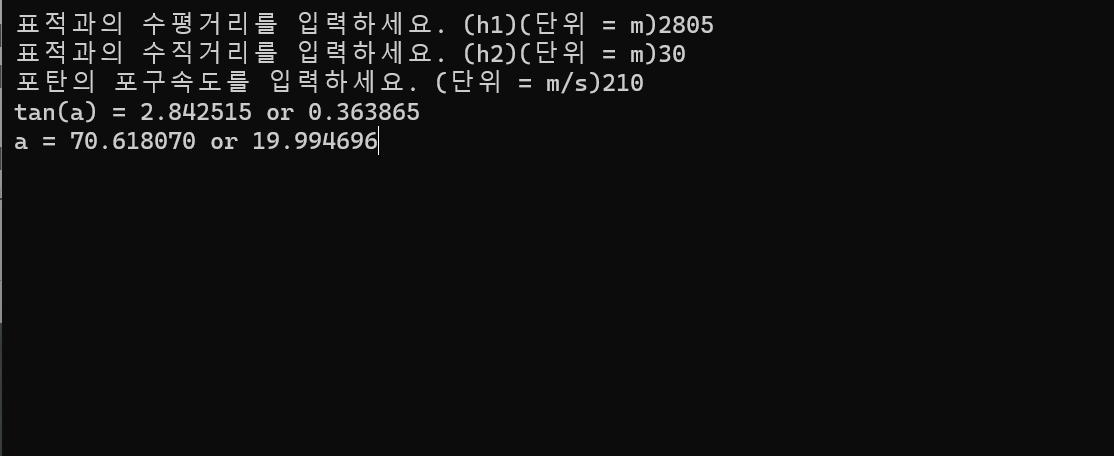
다음과 같은 각도를 얻을 수 있습니다.
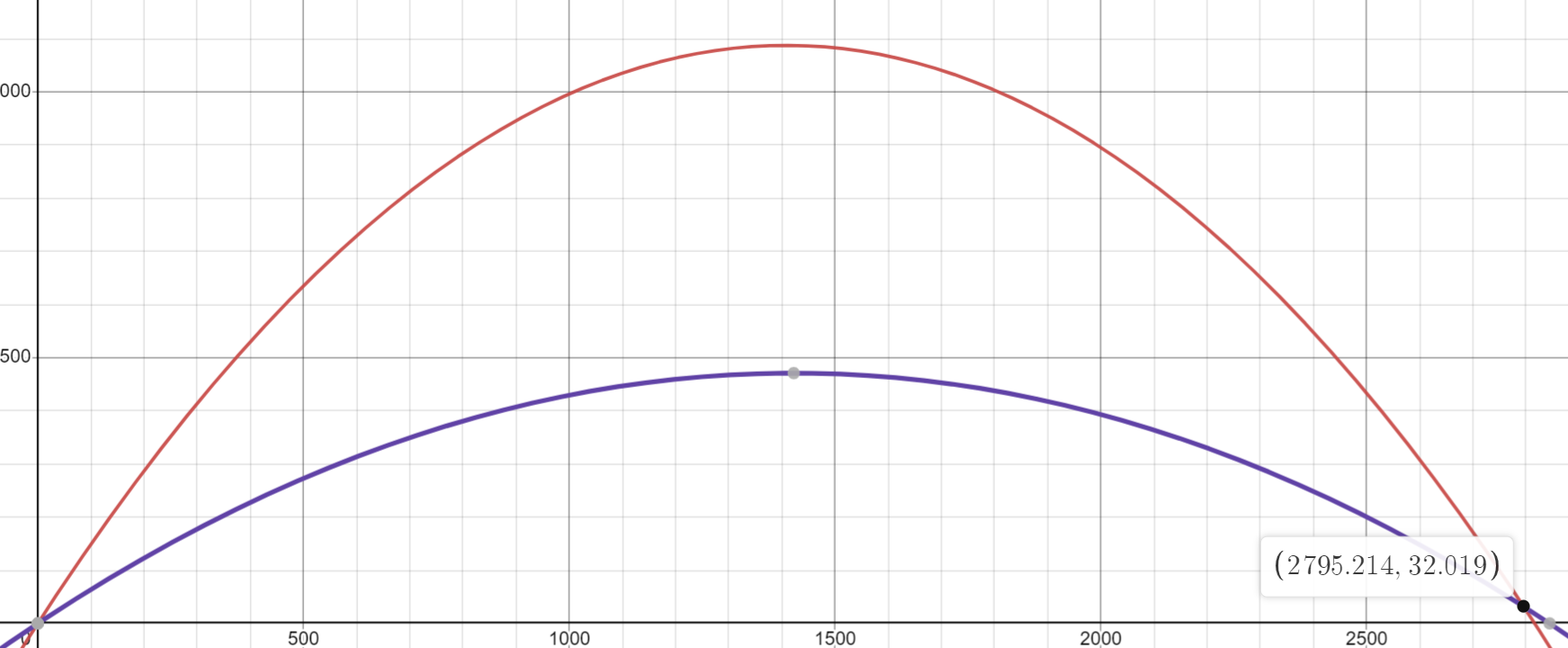
이를 시각화 해보면...
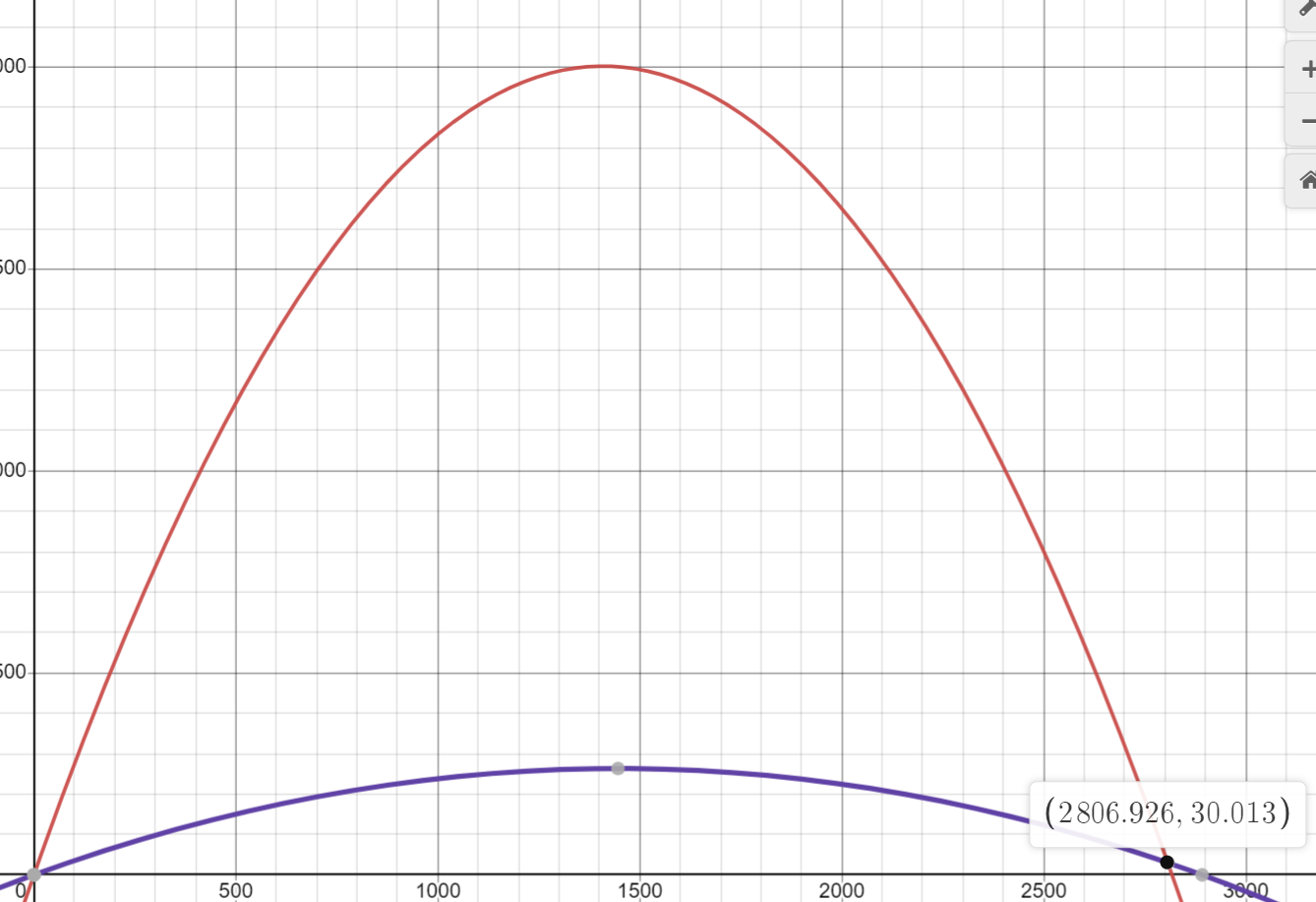
다음과 같이 어느 정도 잘 계산된 것을 알 수 있습니다.
3. 결말
수학과 물리학으로 무장한 김모씨(16세, 미필)
앞에서 계산한 대로 고도각 70.61도로 박격포를 정렬하여 모든 학생의 염원을 담아 발사하게 되는데...
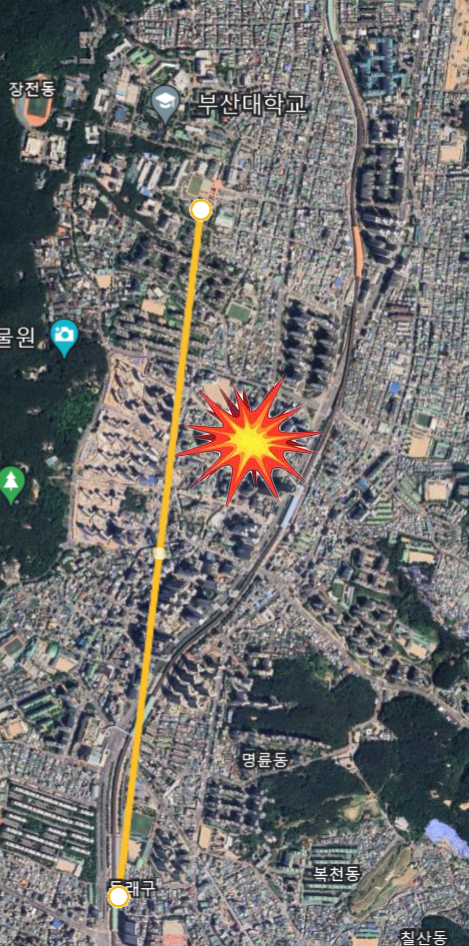
하지만 부산대까지 가지 못한 체 아파트 단지에 떨어져 결국 교도소로 갔다고 한다...
4. 문제점
우리가 계산한 것은 오직 중력만을 고려하는 진공탄도방정식을 이용하였기 때문에 공기저항이나 바람, 지구의 회전등은 계산되지 않았습니다.
따라서 오차가 많이 발생할 수 밖에 없습니다.
자세한건 「총과 탄도학」(2001. 01. 31), 청문각을 참조하세요. 절판되긴 했지만, 학교 도서관에 뒤져보면 하나쯤 있더라고요.

여러분들도 수학과 물리학 지식만 있다면 학교를 날려버릴수 있으니 한번 도전해 보세요.
※ 주의 ※
위의 이론은 어디까지나 이론일 뿐 실제 박격포에 사용하시면 안됩니다. 잘못된 점이나 오류 등이 존재할 수 있고, 만약 있으면 댓글로 남겨주세요.
'소프트웨어' 카테고리의 다른 글
| 노벨피아 부수기 #2 (데이터 분석) (4) | 2024.03.20 |
|---|---|
| 노벨피아 부수기 #1 (데이터 스크래핑) (0) | 2024.03.20 |
| 전장의 신 시뮬레이터(cmd 게임) (2) | 2024.02.27 |



